量子拓扑是什么？

量子拓扑(Quantum Topology)和拓扑量子(Topology Quantum)有区别吗?

跟凝聚态有关。

抛个砖。

在物理中2维拓扑不变性源于基态的Z_2对称性破缺。举个例子，超对称基态对称性破缺给出了非平凡威腾指标（Witten Index）;2维非线性西格玛量子场论的狄拉克算子的基态对称性破缺给出了非平凡的狄拉克指标（Dirac Index）。

题主问的前者大概是一个数学物理分支，后者大概是个物理分支。对此我持保留意见，没有查到有用的信息。

小弟没有足够知识回答这个问题，但可以讨论一下。

量子拓扑（Quantum Topology）应该是数学物理的工具，不懂；而拓扑量子场论就是场论，当中涉及拓扑不变量。这在凝聚态物理中十分重要。

那些拓扑绝缘体（topological insulator）或分子数量子霍尔效应（fractional quantum Hall effect）之类的东西，还请相关的高人补上。

低维物理中我们有Kosterlitz-Thouless相变。根据Mermin-Wagner定理，二维系统不存在有序态（ordered state），即没有长程关联（long-range correlation）；可是在XY模型会出现Kosterlitz-Thouless相变，在低温状态下会出现准长程关联（quasi-long-range correlation），实现这种情况的，便是一种拓扑组合：vortex，他们在低温时，vortex会一对对出现，造成准长程关联（即关联函数为），但当过了一个临界温度（critical temperature）时，这些vortex对便会分解，造成短程关联（即关联函数为）；如果没有vortex，关联函数便变成发散。为什麽vortex是拓扑物体呢？因为我们可以求出winding number，而且winding number在任何连续变形下下改变不了。（数学上来讲，就是如果你求这系统的微分方程中引入了winding number vortex，那你无法在这方程求出无vortex或其他q值vortex的解。）

另外，在缧旋磁石（helimagnet）系统中亦出现Skyrmion，在特定的温度和作用磁场下，会出现二维、柱状、蜂蜜形的Skyrmion crystal，每一个Skyrmion都是拓扑物体，winding number可用求，此量也是在任何连续变形下下改变不了。这个现在明白了的东西不多。不过在Pauli型式表示的vortex，变换成三体磁石便成了Skyrmion。

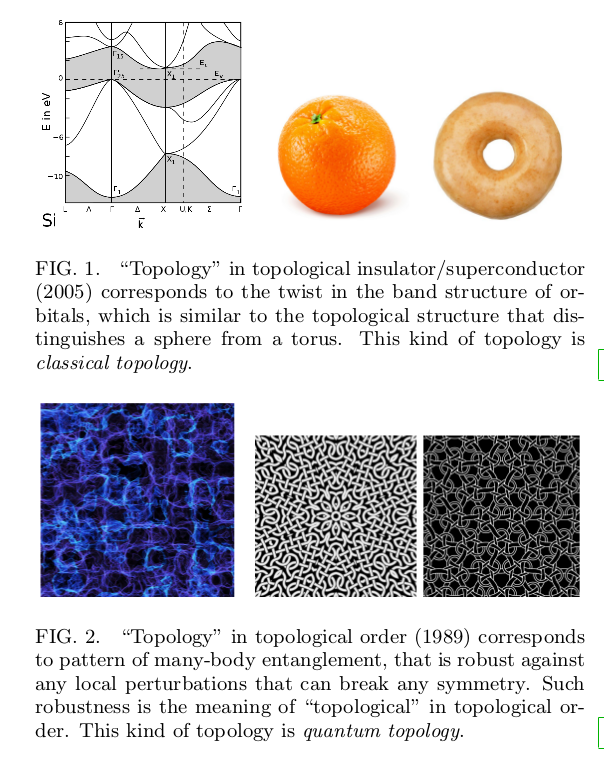
这两个图讲了什么是经典拓扑，什么是量子拓扑。